Solana/Private Key, Public Key and Address/A Cryptographic Explanation of Private Key (Part 3)
The secp256k1 is the elliptic curve used by Bitcoin, based on the Koblitz curve (y² = x³ + ax + b). Its parameters are similar to those recommended by the U.S. National Institute of Standards and Technology (NIST) for the P-256 curve but with some minor modifications. Its equation is:
y² = x³ + 7
In the real number field, its graph is a symmetric curve.
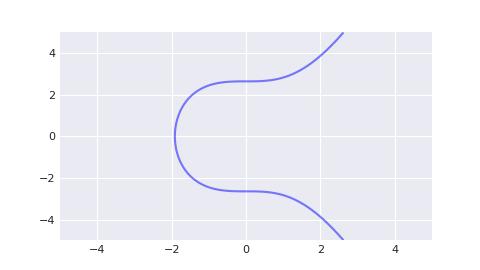
P-256 is another widely used elliptic curve. The difference between secp256k1 and P-256 lies only in their parameters.
Secp256k1 Curve
Secp256k1 is actually a technique based on a finite field of prime numbers. The prime number is equal to:
# Equals to 2**256 - 2**32 - 2**9 - 2**8 - 2**7 - 2**6 - 2**4 - 1
P = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
We can use python to realize the equation for secp256k1.
# Prime of finite field.
P = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
class Fq(Fp):
p = P
A = Fq(0)
B = Fq(7)
class Pt:
def __init__(self, x: Fq, y: Fq) -> None:
if x != Fq(0) or y != Fq(0):
assert y ** 2 == x ** 3 + A * x + B
self.x = x
self.y = y
Q: Given the following (x, y), please determine whether it is on the secp256k1 curve.
import pabtc
x = pabtc.secp256k1.Fq(0xc6047f9441ed7d6d3045406e95c07cd85c778e4b8cef3ca7abac09b95c709ee5)
y = pabtc.secp256k1.Fq(0x1ae168fea63dc339a3c58419466ceaeef7f632653266d0e1236431a950cfe52a)
A:
assert y ** 2 == x ** 3 + A * x + B
Secp256k1 Points Addition
Points on an elliptic curve can form an additive group. Given two distinct points p and q on an elliptic curve, the addition r = p + q is given by the following rule.
- When p == -q, p(x₁, y₁) + q(x₂, y₂) = r(x₃, y₃), r is called the identity element, where
x₃ = 0
y₃ = 0
- When p == +q, p(x₁, y₁) + q(x₂, y₂) = r(x₃, y₃), where
x₃ = ((3 * x₁² + a) / (2 * y₁))² - x * x₁
y₃ = ((3 * x₁² + a) / (2 * y₁)) * (x₁ - x₃) - y₁
- When p != ±q, p(x₁, y₁) + q(x₂, y₂) = r(x₃, y₃), where
x₃ = ((y₂ - y₁) / (x₂ - x₁))² - x₁ - x₂
y₃ = ((y₂ - y₁) / (x₂ - x₁)) * (x₁ - x₃) - y₁
Secp256k1 Points Scalar Multiplication
The addition has been defined, and we can define scalar multiplication next. Given a point p and a scalar k, then p * k equals the sum of adding p repeatedly k times arithmetically. The multiplication on elliptic curves can be decomposed into a series of double and add operations. For example, to compute 151 * p, we would intuitively perform 150 point additions; however, this can be optimized.
The number 151 in binary is represented as 10010111:
151 = 1 * 2⁷ + 0 * 2⁶ + 0 * 2⁵ + 1 * 2⁴ + 0 * 2³ + 1 * 2² + 1 * 2¹ + 1 * 2⁰
Specifies that the initial result is 0. We start from the least significant bit of 10010111. If a bit is 1, we add p to the result; if it's 0, we set p = 2p. The following Python code demonstrates this:
def bits(n):
# Generates the binary digits of n, starting from the least significant bit.
while n:
yield n & 1
n >>= 1
def double_and_add(n, x):
# Returns the result of n * x, computed using the double and add algorithm.
result = 0
addend = x
for bit in bits(n):
if bit == 1:
result += addend
addend *= 2
return result
Secp256k1 Generator
We define a special point called the generator g, such that any point on the elliptic curve can be expressed as g multiplied by a scalar k.
G = Pt(
Fq(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798),
Fq(0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8),
)
Secp256k1 Order
The number of points on an elliptic curve is referred to as its order. The scalar k must be less than this value. For the secp256k1 curve, this limit is:
# The order n of G.
N = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
Secp256k1 Code
In conclusion, we have the complete secp256k1 code below. You can find this code in pabtc.secp256k1.
# Prime of finite field.
P = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
# The order n of G.
N = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
class Fq(Fp):
p = P
class Fr(Fp):
p = N
A = Fq(0)
B = Fq(7)
class Pt:
def __init__(self, x: Fq, y: Fq) -> None:
if x != Fq(0) or y != Fq(0):
assert y ** 2 == x ** 3 + A * x + B
self.x = x
self.y = y
def __add__(self, data: typing.Self) -> typing.Self:
# https://www.cs.miami.edu/home/burt/learning/Csc609.142/ecdsa-cert.pdf
# Don Johnson, Alfred Menezes and Scott Vanstone, The Elliptic Curve Digital Signature Algorithm (ECDSA)
# 4.1 Elliptic Curves Over Fp
x1, x2 = self.x, data.x
y1, y2 = self.y, data.y
if x1 == Fq(0) and y1 == Fq(0):
return data
if x2 == Fq(0) and y2 == Fq(0):
return self
if x1 == x2 and y1 == +y2:
sk = (x1 * x1 + x1 * x1 + x1 * x1 + A) / (y1 + y1)
x3 = sk * sk - x1 - x2
y3 = sk * (x1 - x3) - y1
return Pt(x3, y3)
if x1 == x2 and y1 == -y2:
return I
sk = (y2 - y1) / (x2 - x1)
x3 = sk * sk - x1 - x2
y3 = sk * (x1 - x3) - y1
return Pt(x3, y3)
def __eq__(self, data: typing.Self) -> bool:
return all([
self.x == data.x,
self.y == data.y,
])
def __mul__(self, k: Fr) -> typing.Self:
# Point multiplication: Double-and-add
# https://en.wikipedia.org/wiki/Elliptic_curve_point_multiplication
n = k.x
result = I
addend = self
while n:
b = n & 1
if b == 1:
result += addend
addend = addend + addend
n = n >> 1
return result
def __neg__(self) -> typing.Self:
return Pt(self.x, -self.y)
def __repr__(self) -> str:
return json.dumps(self.json())
def __sub__(self, data: typing.Self) -> typing.Self:
return self + data.__neg__()
def __truediv__(self, k: Fr) -> typing.Self:
return self.__mul__(k ** -1)
def __pos__(self) -> typing.Self:
return Pt(self.x, +self.y)
def json(self) -> typing.Self:
return {
'x': self.x.json(),
'y': self.y.json(),
}
# Identity element
I = Pt(
Fq(0),
Fq(0),
)
# Generator point
G = Pt(
Fq(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798),
Fq(0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8),
)
In this context, the scalar k corresponds to the secp256k1 private key. The generator point multiplied by k, i.e., g * k, represents the secp256k1 public key. Computing the public key from the private key is straightforward; however, deriving the private key from the public key is computationally very difficult.
Exercise
Q: Given a Bitcoin private key of 0x5f6717883bef25f45a129c11fcac1567d74bda5a9ad4cbffc8203c0da2a1473c, find the public key.
A:
import pabtc
prikey = pabtc.secp256k1.Fr(0x5f6717883bef25f45a129c11fcac1567d74bda5a9ad4cbffc8203c0da2a1473c)
pubkey = pabtc.secp256k1.G * prikey
assert(pubkey.x.x == 0xfb95541bf75e809625f860758a1bc38ac3c1cf120d899096194b94a5e700e891)
assert(pubkey.y.x == 0xc7b6277d32c52266ab94af215556316e31a9acde79a8b39643c6887544fdf58c)