Solana/Private Key, Public Key and Address/A Cryptographic Explanation of Private Key (Part 6)

The Ed25519 is the hottest secp256k1 replacement in recent years. Its development came about by accident. Since its publication in 2005, the 25519 series of curves had been in an unheard of existence in the industry, but the turning point came in 2013, when people discovered that there might be an algorithmic backdoor in the p-256 curves pushed by the U.S. Security Agency, following the Snowden revelations Prism Program. After that, the industry began to try to use the 25519 series of curves instead of the p-256 series of curves.

The Secp256k1 curve belongs to the class of p-256 curves, and only a few parameters have been modified compared to the original.

So far, the promotion and application of the Ed25519 curve has been very successful. Traditional web2 products, such as github and binance, support ed25519 as their api authority verification algorithm. Emerging web3 products, such as solana, also use ed25519 as their core signature algorithm.

Ed25519 Curve

Ed25519 is a twisted edwards curve (ax² + y² = 1 + d * x² * y²) whose expression is:

-x² + y² = 1 - (121665 / 121666) * x² * y²

It is based on the prime number field like secp256k1, but it uses the prime number p as 2²⁵⁵ - 19. If this prime is expressed in hexadecimal, it ends in ed, and the hexadecimal representation of the order of the elliptic curve also ends in ed. Thus ed25519 contains both the author's name, Edwards, and the curve's prime field and order, so the author is a real naming genius. If we were half as good as the author, we wouldn't have to worry about naming variables.

The so-called twisted edwards curve refers to adding a constant term a to the edwards curve (x² + y² = 1 + d * x² * y²), which will "twisted" the edwards curve. The original edwards curve is a very beautiful binary quadratic curve. For example, when d = -30, the edwards curve graph is as follows.

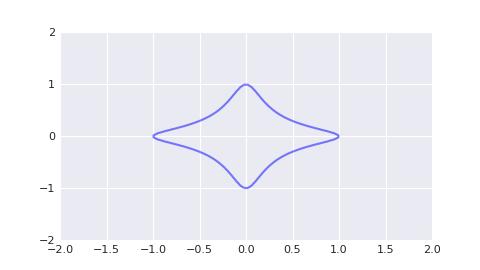
Since the graph of the ed25519 curve is not very intuitive, we use the twisted edwards curve when a = 8, d = 4 as an alternative graph, as shown below.

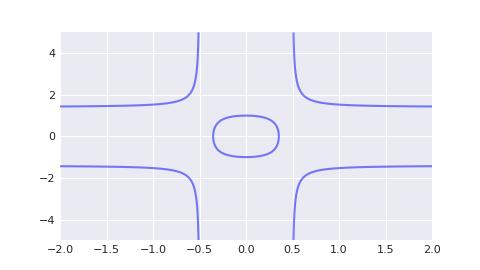
Edwards curve is an alternative elliptic curve. It formally simplifies the addition of points on an elliptic curve, making it easier to implement and more computationally efficient.

All twisted edwards curves are rationally equivalent to the montgomery curve (b * y² = x³ + a * x² + x) in both directions, and the montgomery curve corresponding to ed25519 is called curve25519, and has the following expression. Its image is also very unintuitive, so here we give an alternative image for a = 2.5, b = 0.25.

y² = x³ + 486662 * x² + x

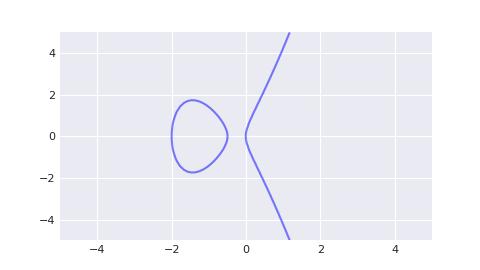
For these different types of elliptic curves, you can understand that the general form of an elliptic curve is y² = x³ + ax + b, which was introduced independently by Koblitz and Miller in 1985. In 1987, Montgomery proved that montgomery curves are bi-directionally rationally equivalent to elliptic curves in general form, and thus montgomery curves are also known as the montgomery representation of elliptic curves. Later in 2005, Edwards proved that twisted edwards curves are rationally equivalent to montgomery curves in both directions, so twisted edwards curves are also called twisted edwards representations of elliptic curves.

Q: Determine if the following point is on ed25519.

x = 0x1122e705f69819df8042c3a34d5294668f25830f41e9b585b2aa6b05ef4cc7e2
y = 0x2a619802432fe95214ac6fed9d01dd149d197f1202e8c2698caab03831b8f2ee

A: Ed25519 is very similar to the code implementation of secp256k1, and you can find its source code in pxsol.ed25519. Alternatively, use pip install pxsol to install the full solana package.

import pxsol

x = pxsol.ed25519.Fq(0x1122e705f69819df8042c3a34d5294668f25830f41e9b585b2aa6b05ef4cc7e2)
y = pxsol.ed25519.Fq(0x2a619802432fe95214ac6fed9d01dd149d197f1202e8c2698caab03831b8f2ee)

assert pxsol.ed25519.A * x * x + y * y == pxsol.ed25519.Fq(1) + pxsol.ed25519.D * x * x * y * y

Ed25519 Points Addition

Similar to the secp256k1 curve, the points on ed25519 can form an additive group. Given two different points p and q on ed25519, the addition r = p + q is given by the following rule.

x₃ = (x₁ * y₂ + x₂ * y₁) / (1 + d * x₁ * x₂ * y₁ * y₂)
y₃ = (y₁ * y₂ - a * x₁ * x₂) / (1 - d * x₁ * x₂ * y₁ * y₂)

The code implementation is as follows.

A = -Fq(1)
D = -Fq(121665) / Fq(121666)

class Pt:

    def __init__(self, x: Fq, y: Fq) -> None:
        assert A * x * x + y * y == Fq(1) + D * x * x * y * y
        self.x = x
        self.y = y

    def __add__(self, data: typing.Self) -> typing.Self:
        # https://datatracker.ietf.org/doc/html/rfc8032#ref-CURVE25519
        # Points on the curve form a group under addition, (x3, y3) = (x1, y1) + (x2, y2), with the formulas
        #           x1 * y2 + x2 * y1                y1 * y2 - a * x1 * x2
        # x3 = --------------------------,   y3 = ---------------------------
        #       1 + d * x1 * x2 * y1 * y2          1 - d * x1 * x2 * y1 * y2
        x1, x2 = self.x, data.x
        y1, y2 = self.y, data.y
        x3 = (x1 * y2 + x2 * y1) / (Fq(1) + D * x1 * x2 * y1 * y2)
        y3 = (y1 * y2 - A * x1 * x2) / (Fq(1) - D * x1 * x2 * y1 * y2)
        return Pt(x3, y3)

Comparing to addition on secp256k1, we see that the addition algorithm on ed25519 is drastically simplified: we don't need additional logic code to determine whether p is equal to ±q. For computers, each additional branching judgment slows down the cpu considerably, so the addition algorithm on the ed25519 curve is very efficient compared to secp256k1.

Ed25519 Points Scalar Multiplication

With addition we can implement scalar multiplication, which will not be repeated here.

Ed25519 Genarator

We define a special point called the generator g, such that any point on the elliptic curve can be expressed as g multiplied by a scalar k.

G = Pt(
    Fq(0x216936d3cd6e53fec0a4e231fdd6dc5c692cc7609525a7b2c9562d608f25d51a),
    Fq(0x6666666666666666666666666666666666666666666666666666666666666658),
)

Q: Calculate the value of g * 42.

A:

import pxsol

p = pxsol.ed25519.G * pxsol.ed25519.Fr(42)

assert p.x == pxsol.ed25519.Fq(0x5dbe6cc3ccfe19f056f503fd5895e4ca00385a5f109126914b52446017318069)
assert p.y == pxsol.ed25519.Fq(0x4237066783c4352092fdf0de4df92cae7343f40939f32b3e195c834e99321ace)